티스토리 뷰

간단 후기 : 난이도 배치가 예년과 달라졌다. 작년까지는 1, 2번에서 거의 만점자 1000명씩 나왔는데 이번에는 2번 문제 보고 '헉' 소리가 나왔다. 그래도 전체적으로 문제가 재밌어서 좋다.
동방에서 SCPC 쳤는데 정말 집중이 하나도 안되는 분위기였지만... 그래도 어찌저찌 잘 했다 ㅋㅋㅋㅋㅋ 심지어 3번 풀고나서 밥먹고 오니까 누가 맥주까지 사오는 바람에.. 술 한 잔 했습니다..
UPD
https://github.com/cheetose/SCPC2020/tree/master/1round
1차 예선 소스 공개
아무튼 풀이
1. 다이어트
$K$일 동안 밥을 먹는데 점심 $N$종류, 저녁 $N$종류의 식사 중 안겹치게 먹는다고 할 때 점심 칼로리 + 저녁 칼로리의 최대값을 최소화 하는 문제다.
각각 칼로리 순으로 정렬한 다음에 $max(a_i + b_{k+1-i})$를 출력하면 된다. $a_1 \leq a_2 \leq ... \leq a_k$와 $b_1 \geq b_2 \geq ... \geq b_k$를 만족한다고 할 때 아무거나 순서를 바꾼다면 현상태보다는 무조건 손해가 발생하기 때문에 위의 간단한 식이 성립한다.
한 줄 평 : eazy
2. 카드 게임
$n$ 과 $k$가 주어지고, $k$ 이하의 수 $n$개로 이루어진 카드더미 2개가 있다. 두 카드더미 중 하나에서 원하는만큼 카드를 가져간다. 이 때 카드에 쓰여진 수의 합이 $k$ 이하여야 한다. 이 때 $(n+1)^2$개의 상태에 대해서 이기는 상태인지 지는 상태인지 구하면된다.
이기는 상태를 0, 지는 상태를 1이라고 하자. 현재 상태에서 갈 수 있는 모든 곳이 0이라면 무조건 지고, 그렇지 않다면 반드시 이길 수 있다. 현재 상태에서 갈 수 있는 곳들은 미리 전처리를 해두고, 투포인터 느낌으로 업데이트 하면 $O(n^2)$에 답을 구할 수 있다. deque 대충 쓰면 TLE 난다.
한 줄 평 : 이게 왜 2번임..??;; 그리고 만점자 수가 왜이리 많음;;
3. 사다리 게임
$N$개의 세로선과 $k$개의 가로선과 $m$개의 쿼리가 있다. 각 쿼리는 시작점, 도착점으로 이루어져있으며 시작점에서 출발하여 도착점에서 끝나기 위해서는 최소 몇 개의 가로선을 지워야하는지 구하면 된다.
시작점, 도착점, 가로선의 양 끝을 모두 정점으로 생각하고

이런 느낌으로 아래로 가는 간선에는 1의 가중치를, 맞은편의 아래로 가는 간선에는 0의 가중치를 두고 0-1 bfs를 돌리면 쉽게 풀린다.
한 줄 평 : 무난한 문제.
4. 범위 안의 숫자
0~9의 숫자로 이루어진 문자열 $t$가 주어진다. $t$에서 $k$개씩 떼어서 만든 수들의 집합을 $S$라고 하자. $S$의 원소 중에서 $[a,a+m]$에 속한 원소의 개수를 최대화 하는 문제다. 이 때 $t$에서 최대 1개 임의의 숫자를 $1$로 바꿀 수 있다.
어떤 숫자를 $1$로 바꿨을 때 영향을 받는 구간이 굉장히 작다는 것을 이용하는 문제다. 일단 원본에서 가능한 모든 수들을 나열할 때에는 '바뀌어서는 안되는 구간'을 같이 저장해주고, 임의의 위치를 $1$로 바꿨을 때 해당 구간에 대해서는 '어디서 바뀌었는지'를 같이 저장해준다.
이 모두를 몽땅 섞어서 수의 크기 순으로 정렬하면 투포인터를 이용해서 $[a, a+m]$에 속하는 구간을 정할 수 있다. 구간 안의 수의 최대값을 구하기 위해서는 세그먼트 트리에 작업을 해야한다. 투포인터로 업데이트 하면서 원본에서 가져온 수를 볼 때에는 '바뀌어서는 안되는 구간'에 모두 1을 빼주고 $1$로 바꾼 수를 볼 때에는 '바뀐 위치'에 1을 더해준다. 물론 없앨 때는 반대로 해주면 된다. 이는 lazy propagation으로 하면 된다. 현재 보고 있는 구간에 '원본에서 가져온 수'의 개수를 C라고 하면 C+max(0, 세그트리에서 가장 큰 값) 요런 꼴로 답이 나온다. 왜 저렇게 나오는가는 직접 확인해보면 감 잡힐 듯 싶다.
한 줄 평 : 이거 집가는 지하철에서 AC 받음
5. 우범 지역
$n$개의 장소가 있고 각 장소는 $p_i$의 확률로 사고가 터진다. 사고가 터진 장소를 덮는 convexhull을 생각하자. 마지막에 어떤 장소의 위치가 주어질 때 이 위치가 convexhull 내부에 있을 확률을 구하는 문제다.
나는 (1-내부에 없을 확률)을 구해서 풀었다. 우선 마지막에 주어진 위치를 원점으로 만들고 나머지 모든 점들도 평행이동 시키자. 그리고 원점을 기준으로 각도 정렬을 하자. 이제 한바퀴 쭉 돌면서 답을 구해줄 건데, 현재 보고 있는 점을 가장 오른쪽(?)에서 선택한 점이라고 하자.
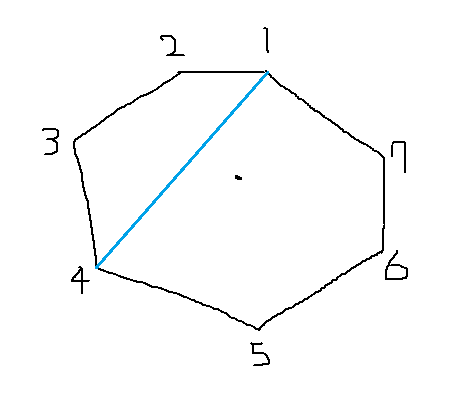
이런 현재 1번 점을 보고 있다고 가정하면 2~4번 점은 사고가 나든 말든 상관 없다. 대신 5~7번 점에서는 절대 사고가 나면 안된다. 따라서 이 경우에는 $p_1(1 - p_5)(1 - p_6)(1 - p_7)$이 된다.
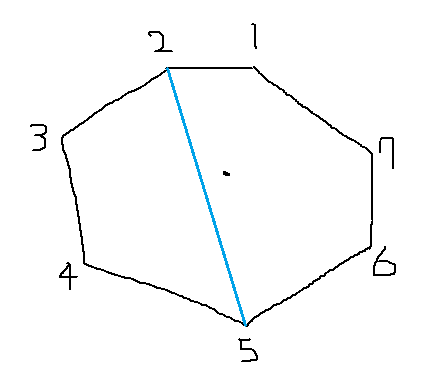
마찬가지로 2번 점을 보고 있을 때에는 3~5번 점은 상관 없고 6~1번 점만 사고가 안나면 된다. 따라서 이 경우에는 $p_2(1 - p_6)(1 - p_7)(1 - p_1)$가 된다. 이런식으로 한 바퀴 돌면서 답을 다 더해주면 된다. $l$번 점을 보고 있을 때 사고와 상관 없는 최대 점을 $r$이라고 할 때 $l+1$번 점에 대한 최대 점은 $r$이상임이 보장된다. (각도 순으로 정렬했기 때문에) 따라서 이것도 투포인터로 사고와 상관없는 구간을 amortized O(1)에 업데이트 할 수 있다.
한 줄 평 : 기.하.싫.어.
'알고리즘 대회' 카테고리의 다른 글
| 2020 ICPC Seoul Regional 후기 및 복기 (8) | 2020.11.15 |
|---|---|
| 뒤늦게 쓰는 ICPC 예선 후기 (5) | 2020.10.18 |
| NYPC 2019 예선 풀이 3~5일차 (0) | 2019.08.18 |
| NYPC 2019 예선 풀이 1~2일차 (0) | 2019.08.17 |
